>

Variables: types, sets and values

As soon as we start to think about a Bayesian modeling, we think about all the possible outcomes of the model. For example, if we want to observe the result of throwing two dice and the sum of them, we may distinguish three variables: $Die_1$, $Die_2$ and $Addition$. The output of the first two variables are numbers between one and six i.e. $Die_1, Die_2\in Type_1=[1, 2,...6]$; the variable $Addition$ is computed in terms of $Die_1$ and $Die_2$, therefore $Addition \in Type_2 = [2, 3,..., 12]$. For example if $Die_1=6$ and $Die_2=3$ then $Addition = 9$. At this point we can make three observations:

1. Two variables types are involved: $Type_1$ and $Type_2$.
2. The variable set $\{Die_1, Die_2, Addition\}$ represents all the outcomes of our system.
3. The variable values $\{Die_1=6, Die_2=3, Addition=9\}$ is a particular output of our model.

Viewed probabilistically, a variable set is an event (e.g. ``observe the result of throwing two dice and the sum of them'') and a variable values is and element of the event (``we got a six in the first die, a three in the second and nine is the sum''). Given a variable set (event) we can be interested in observing just a subset of it. In other words, we are interested in observing just some of the variables. Note that the observed variables are, another event (e.g. ``observing the sum of the two dice''). Briefly, a Bayesian model with a variable set $\Omega$ must be capable of:

1. Providing the probability distribution function of any subset (event) of $\Omega$ , e.g.

   
   

   $$\begin{array}{l} P(\{Die_1, Die_2, Addition\}) \\ P(\{Die_1, Die_2\}) \\ P(\{Addition\})\\ \end{array}$$
   
   

2. Providing the probability of a variable value (element), e.g.

   
   

   $$\begin{array}{l} P(\{Die_1=5, Die_2=4, Addition=9\}) \\ P(\{Die_1=6, Die_2=1\})\\ P(\{Addition=12\})\\ \end{array}$$
   
   

3. Providing the conditional distribution function of any subset (event) $\Omega_s \subseteq \Omega$ given that a variable value (element) $\omega_k \in \Omega_k \subseteq \Omega$ has been observed. e.g.,
   
   $$\begin{array}{l} P(\{Addition\}\vert\{Die_1=6\}) \\ P(\{Die... ...tion=6\} )\\ P(\{Die_2 \}\vert\{Addition=11\} )\\ \end{array}$$
   
   

4. Providing the conditional probability of an element $\omega_s \in \Omega_s \subseteq \Omega$given that an element $\omega_k \in \Omega_k \subseteq \Omega$ has been observed, e.g.
   
   $$\begin{array}{l} P(\{Addition=12\}\vert\{Die_1=6\}) \\ P(\{... ...on=6\} )\\ P(\{Die_2=5 \}\vert\{Addition=11\} )\\ \end{array}$$
   
   

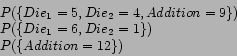
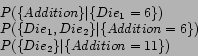
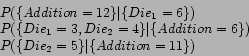
In this way variable type, sets and values are part of the essential information required to construct a Bayesian model. Any question to the model is expressed in terms of variable sets and values. In this chapter we fully describe the construction of variable types, sets and values.