>




: Built-in computable objects
: Variable values
: Loops
目次
索引
In order to introduce some concepts in the following chapters, we now
give some definitions.
Definition 7
The cardinality of an unidimensional variable 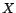 is defined as follows:
is defined as follows:
Definition 8
The order of a variable set of unidimensional variables
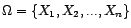 is denoted as
is denoted as 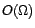 and it
is defined as
and it
is defined as
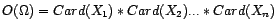 .
.
Juan-Manuel Ahuactzin
平成17年3月31日
![$\displaystyle \left\{
\begin{array}{ll} (max-min) & \mbox{ if } X=[min,max] \\ ...
... } X=<v_0,v_1,...,v_{m-1}> \\
k & \mbox{ if } X=[min:max):k
\end{array}\right.$](img218.png)